Field Rotation & its Impact on imaging
Field Rotation
Field rotation limits the maximum exposure possible with an Alt-Az mount. The field rotation depends upon the latitude of the observer, as well as, the Azimuth angle and Altitude of the object being observed. The following field rotation formula and plot are copied from an excellent discussion of the topic on the RASC Calgary Center and reproduced here in short:
Field Rotation Rate (arcsec/sec) = R = 15.04 (deg/hr) COS(Latitude)*COS(Azimuth Angle) / COS(Altitude Angle)
This equation indicates several key facts about field rotation:
1. For any given Latitude and Azimuth angle, the maximum field rotation occurs at an Altitude of 90 degrees. In other words, at the observer's zenith. Mathematically, there is a singularity at 90 degrees Altitude as the equation goes to infinity. This simply reflects the fact that an Alt-Az mount cannot track field rotation directly overhead.
2. For any given Latitude and Altitude the field rotation is minimal at 90 deg and 270 deg Azimuth, that is due east and due west. Looking in these directions, a star is moving directly toward or directly away from the observer so no star trailing can occur. Of course, this is only a momentary condition but the rotation increases slowly as the object moves away from directly due east or west. In contrast, for a Azimuth angle of 0 (360) deg or 180 deg field rotation is maximum. Here the star is moving perpendicular to the direction we are observing so the full effect is observed.
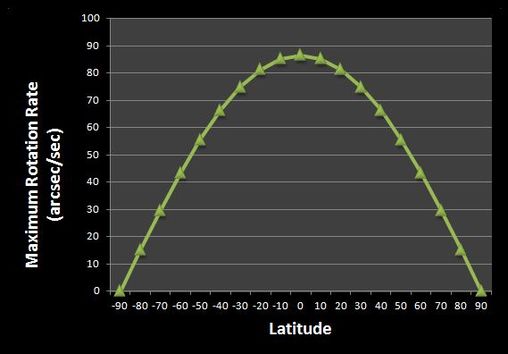
3. With respect to Latitude, field rotation effects are maximum at 0 deg latitude which is the earth's equator, and completely absent at the NCP and SCP, i.e. +/- 90 degress of Latitude. An Alt-Az mount would track the sky perfectly at the poles as the stars will not change altitude as they rotate through Azimuth.
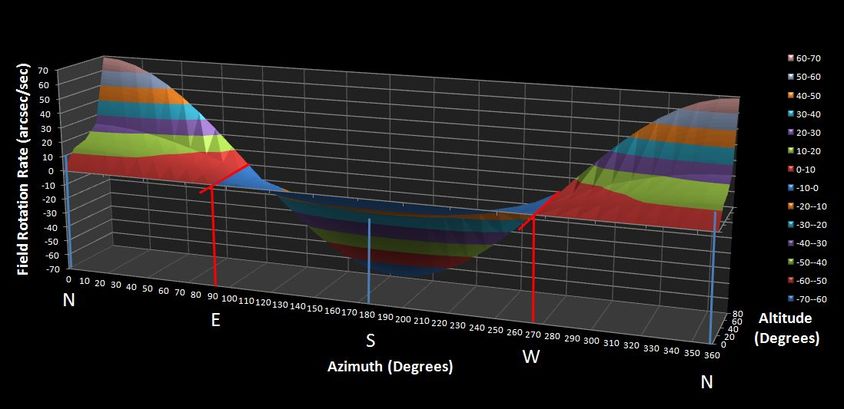
The plot shows the field rotation that you can expect in arcsec per sec for different Azimuth and Altitude angles for an observer at latitude 37 degrees. Field rotation is largest looking north and due south and for objects at higher altitudes. Field rotation is zero due east and due west, but remember the sky is constantly moving so objects in those directions begin to have field rotation immediately. An observer at latitude 37degrees looking at an object at an Altitude of 60 degrees due south, will see the field rotate 24arcsec/sec; while looking at an object in the NE, 45 degrees Azimuth, at an Altitude of 40 degrees will see a field rotation of 11arcsec/sec.
Field rotation limits the maximum exposure possible with an Alt-Az mount. The field rotation depends upon the latitude of the observer, as well as, the Azimuth angle and Altitude of the object being observed. The following field rotation formula and plot are copied from an excellent discussion of the topic on the RASC Calgary Center and reproduced here in short:
Field Rotation Rate (arcsec/sec) = R = 15.04 (deg/hr) COS(Latitude)*COS(Azimuth Angle) / COS(Altitude Angle)
This equation indicates several key facts about field rotation:
1. For any given Latitude and Azimuth angle, the maximum field rotation occurs at an Altitude of 90 degrees. In other words, at the observer's zenith. Mathematically, there is a singularity at 90 degrees Altitude as the equation goes to infinity. This simply reflects the fact that an Alt-Az mount cannot track field rotation directly overhead.
2. For any given Latitude and Altitude the field rotation is minimal at 90 deg and 270 deg Azimuth, that is due east and due west. Looking in these directions, a star is moving directly toward or directly away from the observer so no star trailing can occur. Of course, this is only a momentary condition but the rotation increases slowly as the object moves away from directly due east or west. In contrast, for a Azimuth angle of 0 (360) deg or 180 deg field rotation is maximum. Here the star is moving perpendicular to the direction we are observing so the full effect is observed.
3. With respect to Latitude, field rotation effects are maximum at 0 deg latitude which is the earth's equator, and completely absent at the NCP and SCP, i.e. +/- 90 degress of Latitude. An Alt-Az mount would track the sky perfectly at the poles as the stars will not change altitude as they rotate through Azimuth.
The plot shows the field rotation that you can expect in arcsec per sec for different Azimuth and Altitude angles for an observer at latitude 37 degrees. Field rotation is largest looking north and due south and for objects at higher altitudes. Field rotation is zero due east and due west, but remember the sky is constantly moving so objects in those directions begin to have field rotation immediately. An observer at latitude 37degrees looking at an object at an Altitude of 60 degrees due south, will see the field rotate 24arcsec/sec; while looking at an object in the NE, 45 degrees Azimuth, at an Altitude of 40 degrees will see a field rotation of 11arcsec/sec.
The field rotation rate varies as the cosine of the latitude of the observer. As the graph below shows, this means that the rotation rate is maximum at the equator and zero at the north and south poles as noted above.
 Graphical representation of field rotation lines superimposed
on a grid of pixels in a sensor
Graphical representation of field rotation lines superimposed
on a grid of pixels in a sensor
Photographers Rule of 500
The "Rule of 500" is a simple rule of thumb used by night time photographers (not astrophotographers) to avoid blurring of stars in nighttime images using fixed cameras. The rule simply stated says that the maximum exposure possible without objectionable star trailing is simply obtained by dividing 500 by the system focal length:
Rule of 500 Max Exposure (sec) = 500 / Focal Length (mm)
You will find discussions in the on line astronomy forums which say that the "Rule of 500" is outdated and does not apply to modern day digital cameras. Some substitute "400", "300", or even "100" for the 500. The problem is the 500 rule does not account for pixel size which can vary greatly for different cameras, and even vary for a single camera when binning is used. There is a very nice derivation of the number of pixels that can be traversed without noticeable star trailing which takes into account pixel size. You can read the details here which lead to the equation below: kelly.flanagan.io/astronomy/astrophotography/field-rotation-and-alt-azimuth-mounted-telescopes/
The following formula is the result:
Pxls = Pi x Earth's Rotation (deg/sec) / (360 x Pixel Size (microns) x 10E-6)
Pxls is the allowable number pixels traversed. The Earth's Rotation rate is is 0.00417 deg/sec so the above equation reduces to:
Pxls = 36.4 / Pixel Size(microns)
For a 3.8 micron pixel size as in the ASI1600MC camera, this works out to 9.5 pixels before blurring becomes objectionable. For a video camera like the Mallincam Xtreme with much larger pixels of ~9 microns the number is only 4 pixels before blurring becomes an issue. It makes sense that as the pixel size gets larger, we can tolerate motion across less of them. Instead of any of these photography rules, some people simple cannot tolerate any more than 5 or 7 pixels before star trailing becomes objectionable. The fact is, it really depends upon an individual taste and the magnification at which the image is viewed. Obviously, one can tolerate less pixels if an image is viewed on a large screen where each pixel is magnified.
Maximum Exposure Considering Field Rotation
Pulling all of this together, we can calculate the maximum exposure before star trailing becomes objectionable for any point in the sky if we are using an Alt-Az mount. We must first realize that field rotation will result in stars rotating around the center of our field of view (FOV). In the case of a camera, rotation will be about the center of the sensor as pictured in the diagram here. The further from the center of the sensor the longer the length of the rotation path shown by the progressively larger circles shown. The worst case is at the corners of the sensor. The Path Length traversed is expressed by the following formula:
Path Length = PL = (2 Pi / 360) x d x R x t
where PL is the path length of the star in microns at a distance d in microns from the center of the sensor. R is the field rotation rate in degrees/hr (or arc-seconds per second) from the formula above and t is the length of our exposure in seconds. Substituting the equation for field rotation above and converting from a field rotation rate of degrees/hr to degrees/sec we have:
PL= (2 Pi /360) x d x (15.04/3600) x cos (latitude) x cos (azimuth) x t /cos (altitude)
which reduces to
PL = 0.0000729 x d x cos (latitude) x cos (azimuth) x t / cos (altitude)
Next we can determine how many pixels of motion are involved simply divide by the pixel size, s, in microns.
# Pixels Traversed = PL / s = 0.0000729 x (d/s) x cos (latitude) x cos (azimuth) x t / cos (altitude)
Let us use the example of the ASI1600 camera, it has a sensor array of 4656 x 3520 pixels arranged in a chip which is 23.6mm x 15.6mm. Each pixel is 3.8 micron in size. So the longest distance from center is along the diagonal of the chip which is 14.14mm, or 14,140 microns to be in the same units as the pixel size. With this data the equation for the number of Pixels Traversed becomes:
# Pixels Traversed = PL / s = 0.271 x cos (latitude) x cos (azimuth) x t / cos (altitude)
At a latitude of 37 degrees, looking due south at an Azimuth of 180 degrees, and looking up at an Altitude of 60 degrees the equation becomes:
# Pixels Traversed = 0.271 x cos 37deg x cos 180deg x t / cos 60deg
# Pixels Traversed = 0.433 x t
So if we can tolerate star motion across 7 pixels for this camera and the size of the displayed image, then we can invert the equation to get the maximum tolerable Exposure in seconds:
t = 9.5 / 0.433 = 22 seconds
At an altitude of 80 degrees the maximum exposure is reduced to 7.6 seconds and at 85 degrees it is only 3.8 seconds. On the other hand, looking to the SE at an azimuth of 135 degrees the exposure increases to 30 seconds.
Impact of Chip Size
Now let's look at the impact of chip size on star trailing. Suppose we look at the ASI071 camera which has a pixel size of 4.78 microns and a diagonal of 28.4 mm. As in the first example with the ASI1600 camera, we consider a latitude of 37 degrees, looking due south at an Azimuth of 180 degrees, and looking up at an Altitude of 60 degrees. We must be careful to go back to adjust for pixel size to know the acceptable # of pixels before star trailing becomes intolerable. Now the maximum tolerable time becomes:
t = 7.6 / 0.69 = 11 seconds
Clearly the larger FOV has reduced the maximum exposure with an Alt-Az mount by a factor of 62%. As another example look at the ASI224 with a much smaller chip with a sensor diagonal of 6.09 mm and a pixel size of 3.75 microns. For the same latitude, azimuth and altitude, the maximum tolerable time becomes:
t = 9.7 / 0.12 = 81 seconds
Clearly, a camera with a smaller FOV can handle longer exposures without unacceptable star trailing. This is understood from looking at the different rotation circles shown in the graphic above showing longer star trails for larger chip sizes.
Summary
In summary, an Alt-Az mount will be limited to exposure times determined by the location of the objects being viewed with those at higher altitudes most limited. The typical rule of thumb given is that 30 sec is the maximum, although there are clearly regions of the sky where much longer exposures are possible. And, as chip sizes increase the situation only gets worse.
The "Rule of 500" is a simple rule of thumb used by night time photographers (not astrophotographers) to avoid blurring of stars in nighttime images using fixed cameras. The rule simply stated says that the maximum exposure possible without objectionable star trailing is simply obtained by dividing 500 by the system focal length:
Rule of 500 Max Exposure (sec) = 500 / Focal Length (mm)
You will find discussions in the on line astronomy forums which say that the "Rule of 500" is outdated and does not apply to modern day digital cameras. Some substitute "400", "300", or even "100" for the 500. The problem is the 500 rule does not account for pixel size which can vary greatly for different cameras, and even vary for a single camera when binning is used. There is a very nice derivation of the number of pixels that can be traversed without noticeable star trailing which takes into account pixel size. You can read the details here which lead to the equation below: kelly.flanagan.io/astronomy/astrophotography/field-rotation-and-alt-azimuth-mounted-telescopes/
The following formula is the result:
Pxls = Pi x Earth's Rotation (deg/sec) / (360 x Pixel Size (microns) x 10E-6)
Pxls is the allowable number pixels traversed. The Earth's Rotation rate is is 0.00417 deg/sec so the above equation reduces to:
Pxls = 36.4 / Pixel Size(microns)
For a 3.8 micron pixel size as in the ASI1600MC camera, this works out to 9.5 pixels before blurring becomes objectionable. For a video camera like the Mallincam Xtreme with much larger pixels of ~9 microns the number is only 4 pixels before blurring becomes an issue. It makes sense that as the pixel size gets larger, we can tolerate motion across less of them. Instead of any of these photography rules, some people simple cannot tolerate any more than 5 or 7 pixels before star trailing becomes objectionable. The fact is, it really depends upon an individual taste and the magnification at which the image is viewed. Obviously, one can tolerate less pixels if an image is viewed on a large screen where each pixel is magnified.
Maximum Exposure Considering Field Rotation
Pulling all of this together, we can calculate the maximum exposure before star trailing becomes objectionable for any point in the sky if we are using an Alt-Az mount. We must first realize that field rotation will result in stars rotating around the center of our field of view (FOV). In the case of a camera, rotation will be about the center of the sensor as pictured in the diagram here. The further from the center of the sensor the longer the length of the rotation path shown by the progressively larger circles shown. The worst case is at the corners of the sensor. The Path Length traversed is expressed by the following formula:
Path Length = PL = (2 Pi / 360) x d x R x t
where PL is the path length of the star in microns at a distance d in microns from the center of the sensor. R is the field rotation rate in degrees/hr (or arc-seconds per second) from the formula above and t is the length of our exposure in seconds. Substituting the equation for field rotation above and converting from a field rotation rate of degrees/hr to degrees/sec we have:
PL= (2 Pi /360) x d x (15.04/3600) x cos (latitude) x cos (azimuth) x t /cos (altitude)
which reduces to
PL = 0.0000729 x d x cos (latitude) x cos (azimuth) x t / cos (altitude)
Next we can determine how many pixels of motion are involved simply divide by the pixel size, s, in microns.
# Pixels Traversed = PL / s = 0.0000729 x (d/s) x cos (latitude) x cos (azimuth) x t / cos (altitude)
Let us use the example of the ASI1600 camera, it has a sensor array of 4656 x 3520 pixels arranged in a chip which is 23.6mm x 15.6mm. Each pixel is 3.8 micron in size. So the longest distance from center is along the diagonal of the chip which is 14.14mm, or 14,140 microns to be in the same units as the pixel size. With this data the equation for the number of Pixels Traversed becomes:
# Pixels Traversed = PL / s = 0.271 x cos (latitude) x cos (azimuth) x t / cos (altitude)
At a latitude of 37 degrees, looking due south at an Azimuth of 180 degrees, and looking up at an Altitude of 60 degrees the equation becomes:
# Pixels Traversed = 0.271 x cos 37deg x cos 180deg x t / cos 60deg
# Pixels Traversed = 0.433 x t
So if we can tolerate star motion across 7 pixels for this camera and the size of the displayed image, then we can invert the equation to get the maximum tolerable Exposure in seconds:
t = 9.5 / 0.433 = 22 seconds
At an altitude of 80 degrees the maximum exposure is reduced to 7.6 seconds and at 85 degrees it is only 3.8 seconds. On the other hand, looking to the SE at an azimuth of 135 degrees the exposure increases to 30 seconds.
Impact of Chip Size
Now let's look at the impact of chip size on star trailing. Suppose we look at the ASI071 camera which has a pixel size of 4.78 microns and a diagonal of 28.4 mm. As in the first example with the ASI1600 camera, we consider a latitude of 37 degrees, looking due south at an Azimuth of 180 degrees, and looking up at an Altitude of 60 degrees. We must be careful to go back to adjust for pixel size to know the acceptable # of pixels before star trailing becomes intolerable. Now the maximum tolerable time becomes:
t = 7.6 / 0.69 = 11 seconds
Clearly the larger FOV has reduced the maximum exposure with an Alt-Az mount by a factor of 62%. As another example look at the ASI224 with a much smaller chip with a sensor diagonal of 6.09 mm and a pixel size of 3.75 microns. For the same latitude, azimuth and altitude, the maximum tolerable time becomes:
t = 9.7 / 0.12 = 81 seconds
Clearly, a camera with a smaller FOV can handle longer exposures without unacceptable star trailing. This is understood from looking at the different rotation circles shown in the graphic above showing longer star trails for larger chip sizes.
Summary
In summary, an Alt-Az mount will be limited to exposure times determined by the location of the objects being viewed with those at higher altitudes most limited. The typical rule of thumb given is that 30 sec is the maximum, although there are clearly regions of the sky where much longer exposures are possible. And, as chip sizes increase the situation only gets worse.
© 2024 Curtis V. Macchioni
Proudly powered by Weebly